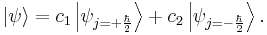Stern–Gerlach experiment

Quantum mechanics
\Delta x\, \Delta p \ge \frac{\hbar}{2}
Uncertainty principle
Introduction · Mathematical formulations
Experiments
Double-slit experiment
Davisson–Germer experiment
Stern–Gerlach experiment
Bell's inequality experiment
Popper's experiment
Schrödinger's cat
Elitzur–Vaidman bomb-tester
Quantum eraser

Important in the field of quantum mechanics, the Stern–Gerlach experiment,[1] named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics. It can be used to demonstrate that electrons and atoms have intrinsically quantum properties, and how measurement in quantum mechanics affects the system being measured.

Contents

Basic theory and description

Basic elements of the Stern–Gerlach experiment.

The Stern-Gerlach experiment involves sending a beam of particles through an inhomogeneous magnetic field and observing their deflection. The results show that particles possess an intrinsic angular momentum that is most closely analogous to the angular momentum of a classically spinning object, but that takes only certain quantized values.

The experiment is normally conducted using electrically neutral particles or atoms. This avoids the large deflection to the orbit of a charged particle moving through a magnetic field and allows spin-dependent effects to dominate. If the particle is treated as a classical spinning dipole, it will precess in a magnetic field because of the torque that the magnetic field exerts on the dipole (see torque-induced precession). If it moves through a homogeneous magnetic field, the forces exerted on opposite ends of the dipole cancel each other out and the trajectory of the particle is unaffected. However If the magnetic field is inhomogeneous, the force on one end of the dipole will be slightly greater than the opposing force on the other end, so that there is a net force which deflects the particle's trajectory. If the particles were classical spinning objects, one would expect the distribution of their spin angular momentum vectors to be random and continuous. Each particle would be deflected by a different amount, producing a smooth distribution on the detector screen. Instead, the particles passing through the Stern-Gerlach apparatus are deflected either up or down by a specific amount. This result indicates that spin angular momentum is quantized (i.e., it can only take on discrete values), so that there is not a continuous distribution of possible angular momenta.

If the experiment is conducted using charged particles like electrons, there will be a Lorentz force that tends to bend the trajectory in a circle (see cyclotron motion). This force can be cancelled by an electric field of appropriate magnitude oriented transverse to the charged particle's path.

Spin values for fermions.

Electrons are spin-1⁄2 particles. These have only two possible spin angular momentum values measured along any axis, +ħ/2 or −ħ/2. If this value arises as a result of the particles rotating the way a planet rotates, then the individual particles would have to be spinning impossibly fast. Even if the electron radius were as large as 14 nm (the classical electron radius), its surface would have to be rotating at 2.3×1011 m/s. The speed of rotation at the surface would be in excess of the speed of light, 2.998×108 m/s, and is thus impossible.[2] Instead, the spin angular momentum is a purely quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles).

For electrons there are two possible values for spin angular momentum measured along an axis. The same is true for the proton and the neutron, which are composite particles made up of three quarks each (which are themselves spin-1⁄2 particles). Other particles have a different number of possible spin values. Delta baryons (Δ++, Δ+, Δ0, Δ−), for example, are spin +3⁄2 particles and have four possible values for spin angular momentum. Vector mesons, as well as photons, W and Z bosons and gluons are spin +1 particles and have three possible values for spin angular momentum.

To describe the experiment with spin +1⁄2 particles mathematically, it is easiest to use Dirac's bra-ket notation. As the particles pass through the Stern–Gerlach device, they are "being observed." The act of observation in quantum mechanics is equivalent to measuring them. Our observation device is the detector and in this case we can observe one of two possible values, either spin up or spin down. These are described by the angular momentum quantum number j, which can take on one of the two possible allowed values, either +ħ/2 or −ħ/2. The act of observing (measuring) corresponds to the operator Jz. In mathematical terms,

|\psi\rangle = c_1\left|\psi_{j = +\frac{\hbar}{2}}\right\rangle + c_2\left|\psi_{j = -\frac{\hbar}{2}}\right\rangle.

The constants c1 and c2 are complex numbers. The squares of their absolute values (|c1|2 and |c2|2)determine the probabilities that in the state |\scriptstyle \psi\rangle one of the two possible values of j is found. The constants must also be normalized in order that the probability of finding either one of the values be unity. However, this information is not sufficient to determine the values of c1 and c2, because they may in fact be complex numbers. Therefore the measurement yields only the absolute values of the constants.

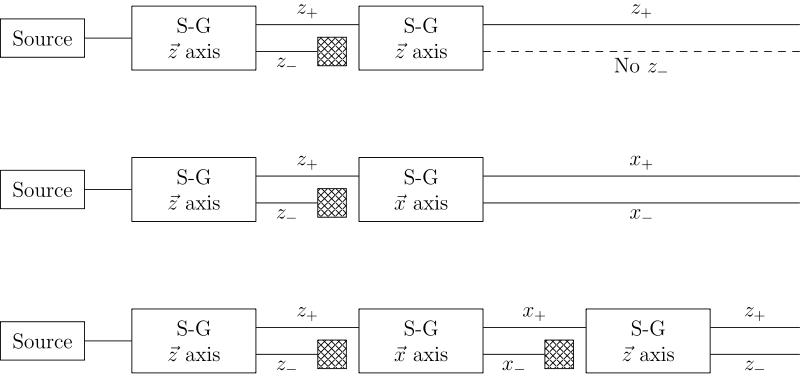
Sequential experiments

If we link multiple Stern–Gerlach apparatuses, we can clearly see that they do not act as simple selectors, but alter the states observed (as in light polarization), according to quantum mechanical law [3]:

Sg-seq.svg


History

A plaque at the Frankfurt institute commemorating the experiment

The Stern–Gerlach experiment was performed in Frankfurt, Germany in 1922 by Otto Stern and Walther Gerlach. At the time, Stern was an assistant to Max Born at the University of Frankfurt's Institute for Theoretical Physics, and Gerlach was an assistant at the same university's Institute for Experimental Physics.

At the time of the experiment, the most prevalent model for describing the atom was the Bohr model, which described electrons as going around the positively-charged nucleus only in certain discrete atomic orbitals or energy levels. Since the electron was quantized to be only in certain positions in space, the separation into distinct orbits was referred to as space quantization. The Stern–Gerlach experiment was meant to test the Bohr–Sommerfeld hypothesis that the direction of the angular momentum of a silver atom is quantized.[4]

Note that the experiment was performed several years before Uhlenbeck and Goudsmit formulated their hypothesis of the existence of the electron spin. Even though the result of the Stern−Gerlach experiment has later turned out to be in agreement with the predictions of quantum mechanics for a spin-1⁄2 particle, the experiment should be seen as a corroboration of the Bohr-Sommerfeld theory.[5].

In 1927, T.E. Phipps and J.B. Taylor reproduced the effect using hydrogen atoms in their ground state, thereby eliminating any doubts that may have been caused by the use of silver atoms.[6] (In 1926 the non-relativistic Schrödinger equation had incorrectly predicted the magnetic moment of hydrogen to be zero in its ground state. To correct this problem Pauli introduced "by hand" so to speak, the 3 spin matrices which now bear his name, but which were then later shown by Dirac in 1928 to be intrinsic in his relativistic equation.)[7]

Impact

The Stern–Gerlach experiment had one of the biggest impacts on modern physics:

See also

References

  1. ↑ Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik 9: 353–355. doi:10.1007/BF01326984. 
  2. ↑ Tomonaga, S.-I. (1997). The Story of Spin. University of Chicago Press. p. 35. ISBN 0-226-80794-0. 
  3. ↑ Sakurai, J.-J. (1985). Modern quantum mechanics. Addison-Wesley. 
  4. ↑ Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik 7: 249–253. doi:10.1007/BF01332793. 
  5. ↑ Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics 26B: 75−86. doi:10.1016/1355-2198(95)00002-B. 
  6. ↑ Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review 29 (2): 309–320. doi:10.1103/PhysRev.29.309. Bibcode: 1927PhRv...29..309P. 
  7. ↑ A., Henok (2002). Introduction to Applied Modern Physics. Lulu.com. p. 76. ISBN 1435705211. 
  8. ↑ Scully, M.O.; Lamb, W.E.; Barut, A. (1987). "On the theory of the Stern–Gerlach apparatus". Foundations of Physics 17: 575–583. doi:10.1007/BF01882788. 

Further reading

External links